This lesson is still being designed and assembled (Pre-Alpha version)

CMSDAS CERN 2020: B2G Long Exercise

Wednesday DAS Plenary 10-11h

Overview

Teaching: 70 min
Exercises: 0 min
Questions
Objectives

From 10h00-11h10 there will be a DAS Plenary, please tune in to that.

Key Points

  • Here is a link to the indico page for Wednesday’s plenary.

Introduction to All-Hadronic b*->tW and Useful Tools

Overview

Teaching: 30 min
Exercises: 20 min
Questions

  • Who are the facilitators and team members?

  • What is this exercise about, and what should we expect from the next few days?

  • Why search for heavy resonances?

  • What is version control and CI/CD?

Objectives

  • Familiarize ourselves with peers and resources.

  • Contexualize a CMS-style search and its stages

  • Understand motivation for physics at high masses/scales.

  • Begin developing new habits with good coding practices.

Introductions

First we can begin with some introductions. The facilitators are:

The team members are:

The overall goal of this long exercise is to offer everyone a high-level exposure of the different components of a physics analysis. In practice, carrying out an analysis takes months and often past a year; we hope to cover the key points of the process and won’t have too much time to do so. To help you through the material, we will be providing some useful code for your use. We strongly suggest you focus on understanding the conceptual flow of the analysis and to ask as many questions as you’d like. We also encourage that you get creative and challenge yourself! If there are any parts of the exercise that you feel you can tackle by writing your own scripts, or optimizing ours, please do! We are all collaborators and we can learn a lot from each other.

Using Git

Before moving on, let’s all get on the same page and test that our workspaces have the packages they need. In the above menu bar, click on Setup and follow the instructions there.

Next, fork+clone the exercise’s repositories. Bookmark the website GitHub repository and the code repository on GitLab. When you navigate to both of these websites, click on the ‘Fork’ button towards the top-right of the page. (You will need to be logged into your GitHub/GitLab accounts)

Question: What is the difference between GitHub and GitLab

You may have noticed that the code repositories hosting the tutorial info and the analysis code used in this exercise use different services (GitHub vs GitLab). Why is this the case?

Solution

GitHub is completely public, whereas GitLab is maintained by CERN and requires credential to host projects. Depending on the needs of the project you are working on, you may want the public nature of GitLab or the speciic tools of GitLab. For example, GitLab’s CI/CD has additional features that are specifically useful to developing analysis software.

Include instructions on how to make sure environment is good to go

Now that you have forked the code onto your personal project space, let’s clone your repository onto your working directory and while we’re at it also set the upstreams:

ssh -Y <LPCUsername>@cmslpc-sl7.fnal.gov
cd ~/nobackup
mkdir CMSVDAS2020
git clone https://github.com/<GitHubUsername>/b2g-long-exercise.git <nameYourTutorialPackage>
cd <nameYourTutorialPackage>
git remote add upstream https://github.com/CMSDAS/b2g-long-exercise.git
git remote -v
cd ..
git clone https://gitlab.cern.ch/<GitLabUsername>/b2g-long-exercise-code.git <nameYourCodePackage>
cd <nameYourCodePackage>
git remote add upstream https://gitlab.cern.ch/cms-b2g/b2g-long-exercise-code.git
git remote -v
cd ..
ls .

Now our code is ready to be worked on.

Good Software Development Habits

Let’s take a few minutes to think about working on software projects as a colloboration. The code you run today (and tomorrow) has been developed by thousands of folks like you trying to make everyone’s life slightly easier. You will probably spend a lot of time reading other people’s code and will quickly build a standard on what ‘good code’ looks like. Similarly when working as a group on a common piece of software, we find good and bad ways to make changes.

To combat these problems, we agree to have a set of ‘good-practices’ for keeping software clean and easy to interpret. First, is the use of comments. When developing a script, begin by stating the code’s intended purpose and a general roadmap to the file. For each function you define (and also important data structures), include in-line comments explaining clearly what the functions/objects are used for. When making commits and merge requests on git, add detailed comments (think about having to sort through dozens of undescribed commits months after pushing them).

Version control is a way of tracing the history of software projects by recording changes encoded in ‘commits/pushes’. We will be using GitHub and CERN’s GitLab to develop our code. CI/CD (Continuous Integrationa and Deployment) is a technique for developing tests on changes (pushes) to the repository. One can, for example, create a test that compiles the code and returns and error if it cannot; one can also create tests for enforcing code style, or execute sample runs of analysis code. The sky is the limit for how fancy you want to make your CI/CD. What do you think should be implemented for our code?

“Homework” (, or bonus part of the lesson)

You should have already forked and cloned your personal version of the repository generating this website. By forking the repository, you have made your own copy of the code which generates a copy of this website, which means you have a tutorial website of your own! (Assuming you haven’t already developed a website with GitHub) To check out your website, go to https://GitHubUsername.github.io/b2g-long-exercise/

In the introduction section at the top of the lesson, you may remember there was a ‘TBA’ space in the (empty) list of participants. The goal of the following execise is to populate that list with brief introductions to you all, by changes you make to your local fork that you will then request to merge into the main website.

The general steps to follow here are:

cd ~/nobackup/CMSVDAS2020/<nameYourTutorialPackage>
git fetch --all
<Enter credentials, (if any) new branches/tags will be made available>
git merge upstream gh-pages
git checkout -b <nameNewBranch>
git branch -v
<Develop code>
git status
git add <fileChanged>
git commit -m 'Write a message describing change'
git push -u origin <nameNewBranch>
<Make Merge(Pull) Request through browser onto main b2g-long-exercises repo>

cd ~/nobackup/CMSVDAS2020/<nameYourTutorialPackage>
<Previous code development>
git branch -v
<If no branch created> git checkout -b <nameNewBranch>
git status
git add <fileChanged>
git commit -m 'Write a message describing change'
git fetch --all
<Enter credentials, new branches/tags are made available>
git rebase upstream gh-pages
git push -u origin <nameNewBranch>
<Make Merge(Pull) Request through browser onto main b2g-long-exercises repo>

Check your websites to make sure the changes look like what you want, it may take a few minutes for the build to update on the site. You can request a pull request through your repository page on GitHub. Before finishing this part of the episode, make sure all repositories are up to date and have the correct latest commit:

cd ~/nobackup/CMSVDAS2020/<nameYourTutorialPackage>
git remote -v
git branch -v

If you do not feel comfortable with git yet, that is ok. This is a learning experience and what we hope you get out of this is being conviced that proper use of versioning is useful when working in a collaboration like CMS. Ask your facilitators for help if you feel stuck, whatever the problem may be, the point of these exercises is to give you ‘big picture’ experiences not coding challenges.

The All-Hadronic b*->tW final state

The b* resonance is a beyond the standard model (BSM) particle that can be produced at the LHC when a b-quark from the incoming proton’s quark-sea interacts with a gluon from the other proton to form an excited resonance that decays to a top-quark and W-boson. The top quark almost always decayse to t->b+W, thus in the final state we have a jet from a b-decay with the W decay jets from the top and the prompt W from the b* decay. It is then the decay channels of the W bosons that determine the final state of the process. In this exercise we will focus on the all-hadronic channel.

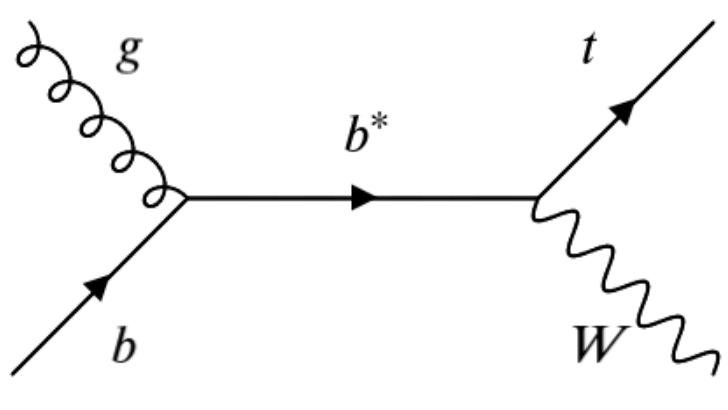
bstarFeynman

In upcoming episodes we will investigate in detail the topology of our signal, as well as possible background standard model (SM) processes that we must model and estimate their expected rates for our search.

Key Points

  • First level of help is at peer-level. The facilitators are here to help for any issues you are unsure about.

  • The big picture is: analyses begin with a motivating final state, then we optimize some selections to keep signal and reject background, finally we consider all systematic uncertainties associated with our selections and modeling in order to quantify the observations we make. Each stage of this process needs dedicated studies and may be performed individually or as a larger team.

  • The LHC and experiments are preparing for Run 3 and HL-LHC; we are exploring models that are motivated by exclusions/measurements made by Run 2 observations.

  • Eliminate fear-of-losing-data by using version control! Commit often, and document, document, document. Save yourself time later by setting CI/CD tests.

Friday DAS Plenary 10-11h

Overview

Teaching: 30 min
Exercises: 0 min
Questions
Objectives

From 10-11h there will be a DAS Plenary, please tune in to that.

Key Points

  • Here is a link to the indico page for Friday’s plenary.

Diving into jet substructure

Overview

Teaching: 20 min
Exercises: 40 min
Questions

  • What is jet substructure?

  • What does the jet substructure look like for the signal?

  • What are some commonly used jet substructure observables for t/W identification?

  • How can jet substructure help combat background and differentiate it from signal?

Objectives

  • Familiarisation with common jet substructure variables.

  • Identify possible discriminating variables for b*->tW signal.

Jets

After collision, colored particles (with a lifetime longer than the hadronization time scale, i.e. not tops) form cone-like hadronic showers as they propagate away from the interaction point. In experiment, we can only see the interactions of the ‘stable’ particles (pions, kaons, etc.) with the detectors, which are on average 2/3 charged particles. The calorimeters measure the energy deposits of these partilces, but we have to decide how to combine those energy deposits to best reconstruct the final state partons. In CMS, we use the Particle Flow technique to define PF candidates which we then cluster into jets.

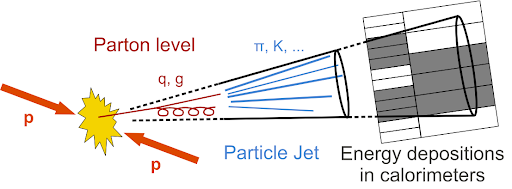
ParticleJet

When analyzing hadronic final states, it is important to understand the jet collections used to cluster energy deposited by the hadronic showers of the final state quarks and gluons. The most common jet clustering algorithm, anti-kt, groups together ‘softer’ (low kT) objects onto harder (high kT) objects recursively until all objects are separated by a distance of the input R-parameter; the R-parameter of a jet defines the maximum radius that it can cluster constituents into itself. Normally, we use R=0.4 to define single-parton jets, e.g. low pT top decays into three separate (resolved) jets.

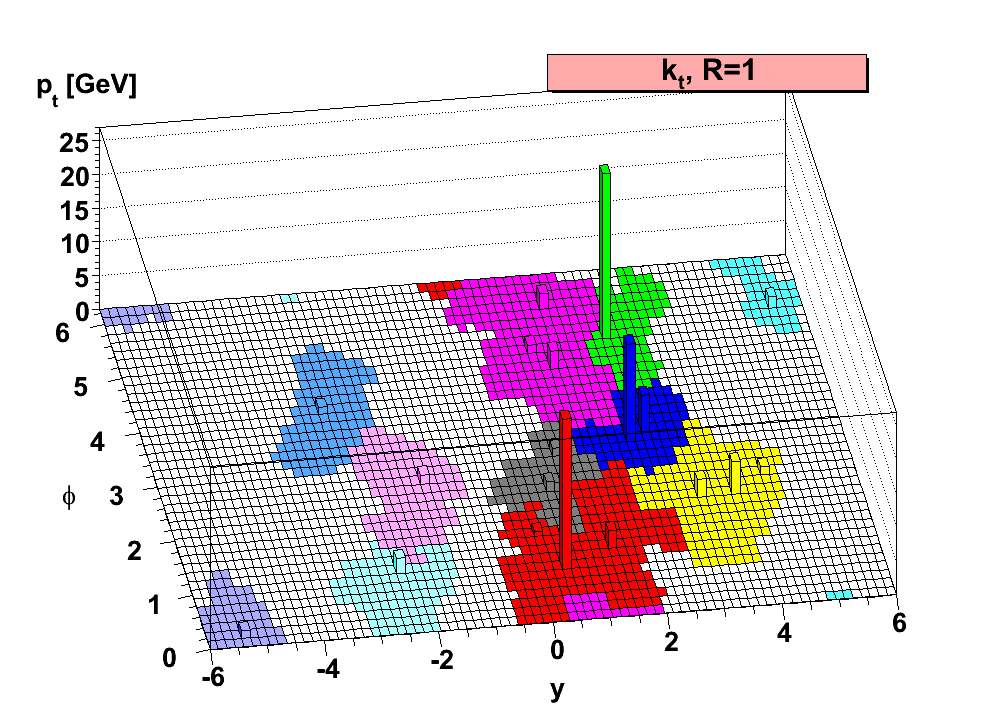
antikt

Sometimes, we want to capture the entire decay of a heavy object using a larger-R jet. The R-parameter used for these puposes depends on the mass and transverse momentum of the decaying particle, and tends to be between R=0.8-1.2. A good rule of thumb is that the opening angle of a massive particle decaying into much lighter constituents is R<2m/pT.

Question: What is are the opening angles for 200 GeV tops? What about 200 GeV Ws? What if they are at high pT ~ 1TeV?

Solution

The useful expression here is R<2m/pT. For a 200 GeV top, R<346/200 -> R<1.73. At the same transverse momentum, a W opens at R<160/200 -> R<0.8. At 1 TeV, the top decays in a cone of about R<0.35 and for the 1 TeV W it is R<0.16. As you may notice, high pT heavy (boosted) objects tend to be well encapsulated by R=0.8 jets. But, at very high pT the decaying objects are quite columnated. The choice of R-parameter for your jet collection, in a way, defines the lower bound of the pT you are sensitive to.

Jet Substructure

Jet substructure is a family of analysis techniques that studies the detailed structure within jets through the constituents of the object. When we cluster PF candidates into anti-kt jets, we can keep the information of which PF candidate is associated with which anti-kt jet. Afterwards, we can calculate substructure observables with the stored information.

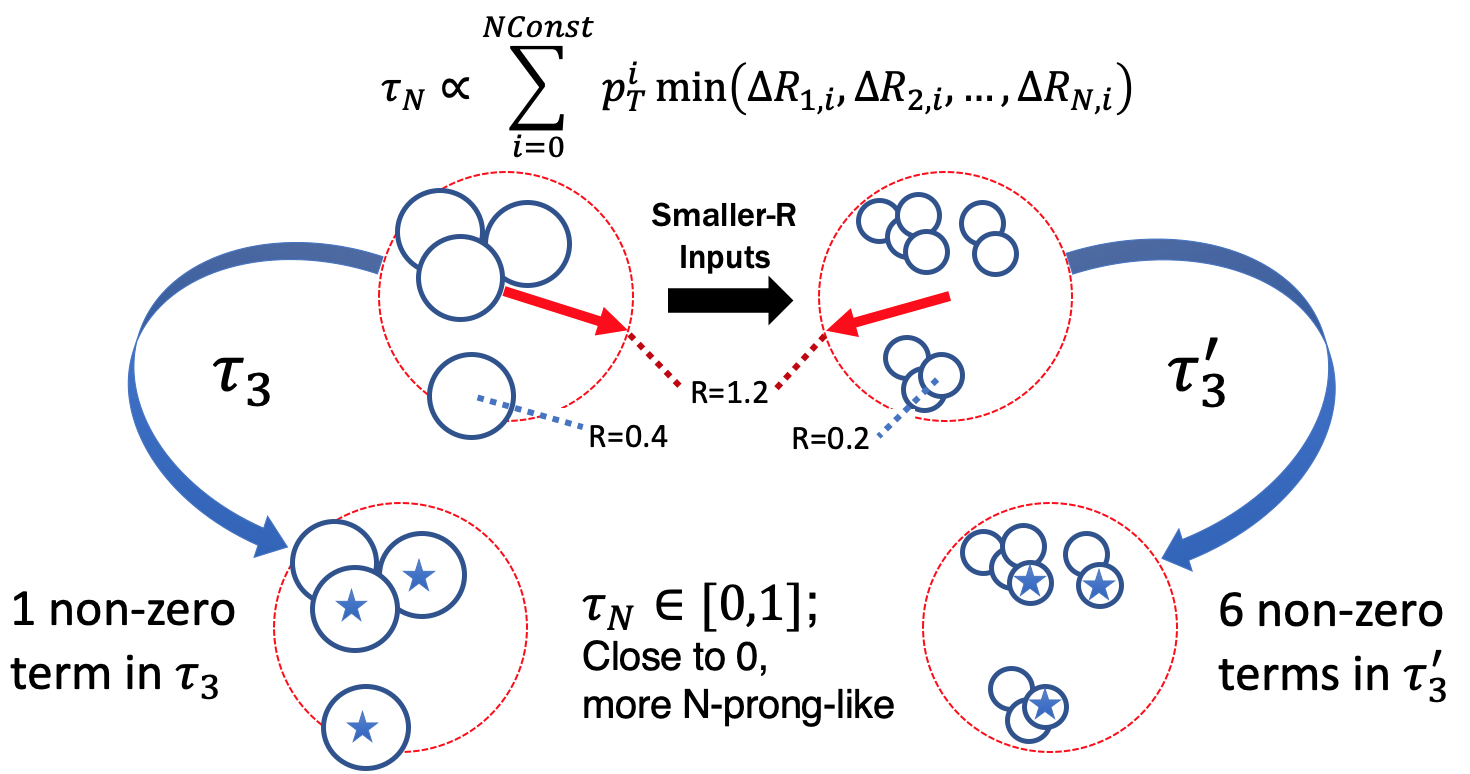
NSubjetinessCartoon

Tops decay (almost always) to b+W, and since we are looking at the all-hadronic channel we are dealing with a W that decays to two quarks. Tagging an all-hadronic top is looking for a 3-pronged jet, where one of those prongs has the decay products of a b-hadron, and typically also requiring the presence of a b-hadron decay and a jet mass close to the 173 GeV of the top quark. W bosons are tagged as two pronged jets in a mass window around 80 GeV.

Question: What jet substructure observables do you think could be used to identify our signal?

Solution

Since we are looking for both a W and a top, we should consider the jet mass. Since our jets will have prong-ed structure, we should consider the N-subjetiness ratios τ32 and τ21. In addition, we can use the impact parameter information (through the form of CSV).

Another way to utilize the constituent information of jets is through the use of Machine Learning models. Below are brief descriptions of some taggers developed within CMS:

Exercise

Use the time before the lunch break to look into the signal sample provided. One quick way to check out its contents is to open the file in interactive root (turning on bash mode with -b helps open the application faster)

root -b /eos/home-l/lcorcodi/Storage/rootfiles/BprimeLH1200_bstar16.root
.ls
_file0->Print()

When loaded from start-up, the file is assigned the ‘_file0’ variable; dig into the information available and see what is available for you to use. Try using the plotting script provided to see some distributions:

cd ~/CMSVDAS2020/CMSSW_11_0_1/src/
cmsenv
cd timber-env
source timber-env/bin/activate
cd ../TIMBER
source setup.sh
cd ../BstarToTW_CMSDAS2020
python exercises/ex4.py -y 16

The very last line calls on the plotting script, and it is using some root files we have already made for y’all. If you would like to change the selections and make the plots, make the appropriate chages to the script and run it with an additional ‘–select’ flag.

Try adding your plots to the B2G-Long-Exercise website through the _extras/figures.md file.

Key Points

  • Jet substructure are analysis techniques for measuring a jet observable through its constituent information.

  • N-subjetiness is how ‘N-pronged’ a jet looks, more specifically for N subjets it is the sum of pt-weighted constuent-subjet spatial moments.

  • Traditional top-tagging typically uses τ32 and jet mass, whereas for W-tagging it’s τ21 and the jet mass.

Investigating the signal topology

Overview

Teaching: 5 min
Exercises: 25 min
Questions

  • What is the signal we are trying to select for?

  • What observables should be investigated for our final state?

  • What do kinematics in the signal look like?

  • How do observables change as a function of resonance mass?

  • Is there an observable that directly probes the signal?

Objectives

  • Familiarisation with the ntuple format.

  • Plot several kinematic variables at parton, particle, and reconstructed level. (Bonus: Investigate relative resolution)

  • Reconstruct the invariant resonance mass.

One of the first questions we should ask ourselves is ‘what does our signal look like?’ Understanding the answer to this will help us decide what selections we should apply to keep as much of the signal as we can, while rejecting as much background as possible. Before making any decisions, we should open up the signal sample we have and get ourselves acquainted with what information is available to us. Sometimes, samples are ‘slimmed’ (removal of unnecessary infomation/branches) or ‘skimmed’ (application of loose selections to reduce number of events) in order to reduce the size of the sample files.

To check the information inside a sample, open it up with root and checkout it’s branches

root -b xrdcp root://cmsxrootd.fnal.gov//eos/store/lcorcodilos/samples/signal.root
.ls
myTree->Print()
myTree->Scan("JetPt")
myTree->Scan("JetPt","JetPt<400")
myTree->Scan("JetPt","JetPt<300")
myTree->Draw("JetPt")

There are more sophisticated ways to investigate the branches available as well as their min/max values in root and python.

Question: Can you find any previous selections that have been applied to the signal sample? If so, why do you think they were done?

Solution

The jet pT has been required to be 350 GeV, and the absolute value of the jet eta (|η|) is 2.5.

Bonus Exercises:

Write a python script that reads the signal sample and outputs each branch name along with the min/max value of that branch into a txt file. Write a pyRoot script that reads the signal sample and outputs plots of each branch, using the min/max values you found above in the binning definition.

You may notice that some variables appear in several variations, e.g. JetPt, PFcandsPt, truthTopPt. What are the different types of collections available (reconstructed, particle, parton, truth, etc.)?

Bonus++: Plot the relative resolutions of the reconstructed objects you have with respect to their truth values. For example, the relative resolution of jet transverse momentum is JER=(recoJetPt-truthJetPt)/truthJetPt

Finally, let’s look into one of the most important observables of the signal: the effective mass of the t+W system.

Key Question

What does this effective mass mean? Does it represent anything physical? Before plotting, what do you think the distribution should look like, and why?

Key Points

  • In an all-hadronic state, we veto leptons (electrons/muons) and study jet properties.

  • Jets are clustered Particle Flow candidates interpreted as a 4-vector with momenta, energy, and mass.

  • The resonance searched decays to all particles in final state, thus if we add all jets in vector-form we can reconstruct the resonance.

Friday Lunch 12-13h

Overview

Teaching: 0 min
Exercises: 60 min
Questions
Objectives

Enjoy your lunch from 12-13h :)

Key Points

Developing a pre-selection

Overview

Teaching: 10 min
Exercises: 50 min
Questions

  • What is the purpose of a preselection?

  • What loose cuts could you apply that follow the signal topology?

  • What are background processes that could enter this selection?

  • How do I normalise background processes?

Objectives

  • Define a ‘good’ region of the detector and apply MET filters.

  • Develop a simple signal selection cutflow.

  • Make stack plots of background processes.

Recording files of this session are in cernbox

Introduction

A preselection serves two purposes, first to ensure that passing events only utilize a “good” region of the detector with appropriate noise filters and second to start applying simple selections motivated by the physics of the signal topology.

Defining a “Good” Region of the Detector

A “good” region of the detector depends heavily on the signal topology. The muon system and tracker extend to about |η| = 2.4 while the calorimeter extends to |η| = 3.0 with the forward calorimeter extending further. Thus, if the signal topology relies heavily on tracking or muons, then a useful preselection would limiting the region to |η| < 2.4. Some topologies, like vector boson fusion (commonly called VBF) have two forward (high eta) jets, so placing a preselection that requires two forward jets is a useful preselection.

cmsDetectorCrossSection

Discuss (5 min)

Now, let’s take a more detailed look at our signal topology and see how it fits in with the detector. The b-star is produced from the interaction of a bottom quark and a gluon, will this production mode yield any characteristic forward jets? In this topology, the b-star decays to a jet from a W boson and a jet from a top quark. What is characteristic of a top jet? What about a W jet? How does this impact the region of the detector needed? What |η| and φ in the detector do we need? Think about this while looking at the Feynman diagram and the signal topology.

bstarFeynman bstarTopo

Solution

The production mode does not have any characteristic forward jets, but the final state has two jets. The top quark decays to a b jet and W jet, where the b jet is typically identified by making use of it’s characteristic secondary vertex. This secondary vertex is identified in the tracker. Both the W jet and top jet have unique substructure that can be used to distinguish them from QCD jets. Therefore it is crucial to use a region of the detector with good tracking and granular calorimetery,so we should restrict |η| < 2.4. There are no detector differences in phi that should impact this search, so there should be no restriction in φ.

Finding Appropriate MET Filters

Missing transverse momentum (called MET) is used to identify detector noise and MET filters are used to remove detector noise. The MET group publishes recommendations on the filters that should be used for different eras of data.

Exercise (5 min)

The recommended MET filters for Run II are listed on this twiki. Use this twiki to create a list of MET filters to use in the preselection.

Simple Selections

The preselection should also include a set of simple selections based on our physics knowledge of the signal topology. These “simple” selections typically consist of loose lower bounds only, which help to reduce the number of events which will get passed to the rest of the analysis while still preserving the signal region.

Consider a heavy resonance decaying to two Z bosons that produce jets to create a dijet final state. In this case, the energy of the collision would go into producing a heavy resonance with little longitudinal momentum, so conservation of momentum tells us that the jets should be well separated in φ, ideally they should have a separation of π in φ. Therefore placing a selection of Δφ > π/2 should not cut out signal, but will reduce the number of events passed on to the next stage.

Reflect

Why not use a selection close to Δφ = π?

Solution

The jets can recoil off of other objects creating a dijet pair that is less than Δφ = π

This also a good stage to place a lower limit on the jet pT. In a hadronic analysis, it is common to place a high lower limit on the pT. For this example, a lower limit of pT = 400 GeV should be good.

Reflect

Why place such a high lower limit on jet pT?

Solution

This is a tricky question. It relates to the trigger. Hadronic triggers have a turn on at high HT or high pT, so the lower limit ensures that that the analysis will only investigate the fully efficient region. triggerTurnOn

A jet originating from a Z boson should also have two “prongs” (regions of energy in the calorimeter), these “prongs” are part of the jet substructure discussed in the earlier lessons. For a two pronged jet like a Z jet, it is good to place a lower limit on the τ21 ratio. Another useful substructure variable to use in the preselection is the softdrop mass. The softdrop algorithm will help to reduce the amount of pileup that is used when measuring the jet mass. The preselection is a good place to define a wide softdrop mass region. For this example, a wide region around the Z boson mass would be ideal, such as 65 < mSD < 115 GeV.

It is important to emphasize that the preselections should be relatively light. It is important to check that the preselection is not eliminating large amounts of signal. A good way to monitor this is to utilize stacked histograms. More about these plots is described below.

Discuss (5 min)

Again, use the images above to think about the signal topology. What “simple” selections can be used in the preselection? Any Δφ or pT criteria? What about substructure?

Solution

In this signal topology the t and W should be well separated, so a light Δφ cut should be placed. Think about a reasonable selection and investigate the result in the plotting exercise. Same for the jet pT. Both the top jet and the W jet should have substructure. The top jet should have three prongs and W jet should have two prongs. Think about the softdrop regions and n-subjettiness (τ) ratios that should be used and investigate them in the plotting exercise.

Applying our selection and monitoring the MC response

When applying the preselection, the selections will be placed serially in the code creating a “cutflow”. The filters are applied first to ensure that the data was taken in “good” detector conditions. Then the kinematic/substructure cuts are applied. It is important to monitor the signal and background in between these physics inspired cuts.

Exercise (20 min) Plots to Monitor Signal and Background

Find where the filters are applied in the exercises/ex4.py script, check that all the filters are there, and then create a histogram displaying τ21 τ32 for the leading and subleading jet. This can be done using the exercises/ex4.py script from the BstarToTW_CMSDAS2020 repository.

cd CMSSW_11_0_1/src # where you saved the TIMBER and BstarToTW_CMSDAS2020 repositories during the setup
cmsenv
python -m virtualenv timber-env
source timber-env/bin/activate
python exercises/ex4.py -y 16 --select

What criteria would you use for τ21? What about τ32?

Solution

The filters are listed as flags

flags = ["Flag_goodVertices",
       "Flag_globalTightHalo2016Filter", 
       "Flag_eeBadScFilter", 
       "Flag_HBHENoiseFilter", 
       "Flag_HBHENoiseIsoFilter", 
       "Flag_ecalBadCalibFilter", 
       "Flag_EcalDeadCellTriggerPrimitiveFilter"]

Then they are applied using the Cut function

# Initial cuts
a.Cut('filters',a.GetFlagString(flags))

Now, we want make histograms for mSD, Δφ, and leading/subleading jet pT.

Let’s modify the ex4.py script to include leading jet pT. To do this, first add a new string to varnames. Then, define the new quantity. Finally, add an if statement to adjust the bounds of the histograms.

# To the varnames
'lead_jetPt':'Leading Jet p_{T}',

# To the definition
a.Define('lead_jetPt','FatJet_pt[jetIdx[0]]')

# add an if statement by the hist_tuple
if "tau" in varname :
    hist_tuple = (histname,histname,20,0,1)
if "Pt" in varname :
    hist_tuple = (histname,histname,30,400,1000)

The histograms for mSD, Δφ, and subleading jet pT are left as homework.

Homework

Make histograms for mSD, Δφ, and subleading jet pT. Then, use these plots to agree on a preselection using the discord chat (Or choose your own if this is after DAS). Finally, add your groups’ decided on preselection to the bs_select.py script in BstarToTW_CMSDAS2020

Key Points

  • Preselection reduces data size, but further signal optimization is done later

  • Preselected events should be in good regions of the detector with appropriate filters

  • Stacked histograms are an important tool for creating cuts

Monday DAS Plenary 10-11h

Overview

Teaching: 30 min
Exercises: 0 min
Questions
Objectives

From 10-11h there will be a DAS Plenary, please tune in to that.

Key Points

Optimising the analysis

Overview

Teaching: 30 min
Exercises: 60 min
Questions

  • What aspects of our analysis do we want to optimize?

  • How can we quantify selections to help decide SR/CR definitons.

  • Do some variables affect signal and BG differently/similarly?

  • Are there any correlated varibles?

  • What final selections are going to be applied to the analysis

Objectives

  • Identify optimizable parts of analysis.

  • Use Punzi significance and other measures to optimise selections.

  • Obtain a close-to-optimal selection to define SR.

Recording files of this session are in cernbox

Setup Ahead of Session

To more efficiently help with debugging, we are going to use remote access of your terminal through tmate. The way this application works is that you can initialize it (by calling ‘tmate’) and it’ll start a session of your terminal that is viewable and editable online. In the website linked it shows how that looks like. If you feel comfortable letting the facilitators use this with you, follow the steps below to install tmate.

To download this you’ll have to use homebrew (another application). To check if you have homebrew installed,

brew help

If you get some output, you’re set. Otherwise it’ll give you an error saying the ‘brew’ command doesn’t exist. In that case, download homebrew by

/bin/bash -c "$(curl -fsSL https://raw.githubusercontent.com/Homebrew/install/master/install.sh)"

Once installed, use homebrew to install tmate by

brew install tmate

In addition, pull all the latest changes from the repositories:

cd ~/CMSVDAS2020/b2g-long-exercise/
git fetch --all
git pull origin gh-pages
cd ../CMSSW_11_0_1/src/
rm -rf timber-env
cmsenv
virtualenv timber-env
source timber-env/bin/activate
cd TIMBER/
git fetch --all
git checkout cmsdas_dev
python setup.py install
source setup.sh
cd ../BstarToTW_CMSDAS2020
git fetch --all
git pull origin master

Wrapping-Up From Preselection Episode

Last session, we talked about how a preselection is useful to cut down the size of the ntuples produced/read. Generally your preselection should include the union of your signal and control regions, cutting out unnecessary data. Later on, we will make further selections to optimize our signal regions and estimate the background in control regions. For this stage, using the plots we were able to make from BstarToTW_CMSDAS2020/examples/ex4.py, let’s decide on a preselection.

Question: What should our preselection be?

Discuss for the next ~15 minutes what the preselection for our analysis should be. Feel free to use your plots as evidence supporting your argument. Think about what the preselection is supposed to be cutting on (e.g., remember to leave space for estimating the BG).

Solution

The pre-selections chosen for the all-had b*->tW (B2G-19-003) analysis were

  • Standard filters and JetID
  • pT(t), pT(W) > 400 GeV
  • |η| < 2.4
  • |Δφ| > π/2
  • |Δy| < 1.6
  • W-tga: τ21 < 0.4/0.45 and 65 < mSD < 105 GeV
  • (Later) mtW > 1200 GeV

Taking a Step Back: Analysis Strategy

With an idea of how we want to make our preselection, let’s take a moment to think ahead to how we want to organize our analysis.

Question: How would we expect to see our signal? Is there a specific, discriminating variable we should be using in our analysis to find our signal?

Think about what kind of signal we are looking for. Is it a resonance or not? What

Solution

We are looking for an excited b-quark resonance (b*). Resonances tend to appear as a ‘bump’ in some observable with a normally falling distribution. For example, in 2012 analysis teams performed a similar strategy when searching for the scalar (Higgs) boson at 125 GeV. HiggsDiscoveryPlot In this example, the mass was reconstructed from the two decaying photons or muons. For our signal, the mass of the b* is also an observable that could help discriminate; we can reconstruct the b* effective mass (mtW) from the decaying t and W.

Now that we know we will want to use mtW, we need to make a rough decision of how we are going to select for signal and estimate the background.

Question: What is our general signal-selection/background-estimation strategy going to be?

Think about what backgrounds we have, how we will estimate those, and how we can make the best selection for a signal region.

Solution

Disclaimer: We are guiding you through the decisions made by the All-Had b*->tW analysis team, y’all are free to differ from it. This is just an example of what was done recently. Our backgrounds are predominantly multi-jet QCD background (including W+Jets), and SM processes with tops+jets (ttbar and singletop). ttbar and singletop are BGs that are fairly well-modeled and we will keep their shape but allow their normalization to float when fitting parameters as the end. We will discuss fitting parameters on Tuesday’s sessions. A simple way would be to use a ‘bump-hunt’ in mtW. We can also use mt, to simultaneously define a signal region and a measurement region for QCD/W+Jets and ttbar. We will discuss this 2-D bump-hunt approach in detail in the next session. We can define the signal region by further optimizing selections on our t and W candidate jets, with a window selection on the mt and bump-hunt in mtW.

Optimizing: But How?

Perhaps when deciding the rough preselection cuts you may have already thought ‘How do I make the best cuts to the variables available to me?’ Another question of similar nature is ‘how would I define what is best?’ There are a few ways to answer these questions, but first we must decide on how we are going to define ‘optimal’ cuts.

Question: How will we define optimal?

What objective measure will we use to help us define an optimal selection?

Solution

One (bad) way to define whether a selection is ‘good’ or ‘bad’ is by simpy asking if it cuts away more signal than it does background. The reason this is not adequate is that you want to make a selection that cuts away background at a rate that enhances the signal significance. Roughly, the significance of the signal strength can be estimated as the ratio of the signal over the square root of the dataset σsig &approx; Nsig/√Ntot&approx;Nsig/√NBG

Going forward with this exercise, we will use the the ‘S/√B’ approximation for significant to guide our decisions.

Tightening Selections

Now that we understand what the minimal selection is that we want to apply to our signal and background, we need to think harder about what are the final (tighter) selections that we want to apply to define our signal and control regions.

Question: What are some parts of the analysis you think could be optimized?

In addition to the preselection, we can make selections on the top and W bosons to ensure an enriched signal region.

Solution

As mentioned above, the pre-selections chosen for the all-had b*->tW (B2G-19-003) analysis were

  • Standard filters and JetID
  • pT(t), pT(W) > 400 GeV
  • |η| < 2.4
  • |Δφ| > π/2
  • |Δy| < 1.6
  • W-tga: τ21 < 0.4/0.45 and 65 < mSD < 105 GeV
  • (Later) mtW > 1200 GeV

Our selections should at-least be this tight. In addition to these selections, the SR of their analysis is defined by a top tag of

  • τ32 < 0.65
  • mSD window of [105,220]
  • deepCSVsubjet < 0.22(2016)/0.15(2017)/0.12(2018) More specifically, the B2G-19-003 team included the mtW > 1200 GeV cut in the later selections and defined the SR W-tagged jet as one that is not top-tagged but passes the preselection cuts. In the case that the two leading jets are top-tagged, this region was used as a ttbar measurement (control) region.

Do we want to use similar selections? Try looking into these distributions and make your own call!

‘N minus 1’ Plots

One powerful analysis tool for optimization are what are referred to as ‘N minus 1’ plots. These are plots of distributions used in series of selections, systematically omitting one selection of the series at a time and plotting that varibale. N-1 plots can help us understand the impact of tightening cuts on the variable. Normally, we ‘tighten’ selections and want to know how our significance estimate changes as a function of ‘tighening’. The direction of ‘tight’ depends on the observable at hand, for example toward 0 for τ32 and towards infinity for jet pT.

Question: How would you define tight for a mass peak?

Solution

Normally we use a one-sided selections, but for a mass peak we may want to make a window requirement. MassSignificance The closer you are to the taregt mass the tighter. Thus, you would have to make a decision on what the target mass should be (note this could differ from the ideal mass) for use as the upper limit of the significance estimation.

Give it a shot yourself, type the following into your terminal from the BstarToTW_CMSDAS2020 directory

python exercises/nminus1.py -y 16  --select

This should create some example plots for the selections used by the B2G-19-003 analysis team. Change the selections applied to what you have decided upon today to checkout the impact of your cuts. Is your selection optimal? Use the remaining time to produce and look into these plots to come up with a signal region selection.

Key Points

  • Preselection is not enough to be sensitive to signal, we need to tighten selection to increase significance of signal to background.

  • The traditional way of optimizing selections is to apply N-1 (all-but one) cuts and findng peak of significance curve in removed cut.

  • Boosted Decision Trees and other multivariate optimization techniques are also widely used.

Monday Lunch 12-13h

Overview

Teaching: 0 min
Exercises: 60 min
Questions
Objectives

Enjoy your lunch from 12-13h :)

Key Points

Controlling the background

Overview

Teaching: 10 min
Exercises: 50 min
Questions

  • What is the background to the search?

  • How can we model the background processes affecting our measurement?

  • Do we have common resources to estimate the background?

  • How can we test our background modeling technique?

  • How and why should we enrich a particular background process when defining control regions?

Objectives

  • Identify background processes affecting current preselection.

  • Understand performance and limitations of background simulations.

  • Develop control regions in which one can estimate individual backgroud processes.

  • Understand the concept of blinding, and have a first look into data in CRs.

Recording files of this session are in cernbox

Backgrounds to the Analysis

We begin understanding our background by considering the final state of the signal. The excited b decays to a top quark and a W boson, where the decays of both are to several jets. bstarFeynman There are are a few Standard Model processes that can lead to a top+W-like experimental signature: – Multi-jet QCD: The nature of the LHC means hadronic background is given for any analysis that does not have a lepton or missing energy to flag. The reason we get large masses in W/t-candidates is that jets cluster any PF candidate within the R-parameter, and with enough momentum and/or distance between PF candidates these QCD events can create a large-mass jet. – W+Jets: This process is when a single W-boson is produced in association to QCD jets. Since the preselection identifies the true W, the process become a background to our signal through its associated jets. Thus, we can include the process as part of the ‘QCD’ (stochastic jets) background contibution. – ttbar: The simplest way this process can enter our signal region is a fully-hadronic decay, where one of the b-quarks is either soft or not identified with our b-tagging. It can also happen that the top has a large decay opening-angle and the W decay is captured in a large-R jet separate from the associated b-quark. – singletop: The Standard Model can have a pair of protons produce a single top in association to a (usually heavy) quark or W-boson. In our case the top produced with a W becomes an irreducible background, however less dominant than the above processes.

Control Regions

Just as signal regions are defined by selections meant to enrich a measurement in signal while eliminating as much background as possible, a control regions are defined by selections meanto to enrich a measurment with a particular background and rejecting as much signal as possible. The idea behind control regions are to provide a kinematic region which is orthogonal but ‘close’ to the signal region, where a particular background is dominant; the MC is then adjusted to match the data in that region and then an extrapolation is done to approximate the MC scalings needed in the signal region to appropriately model the data. The extrapolation could be a single ‘Scale Factor’, or a more sophisticated ‘Transfer Function’

Question: Can you come up with a rough idea for Control Region for any of our background?

Solution

ttbar is arguably the easiest to define a control region for: require having two top-tags. singletop is an irrducible background, it truly has a t and W in the final state. To develop a CR for it one would have to find fine differences in production kinematics, however its sub-dominance to the other BGs makes having a dedicated CR not time-efficient. Multi-Jet Production: The process has a falling distribution across mtop and mtW. The MC is not well-modeled. The best way to model this is to fit a polynomial to the data that extends in both axes. We can measure all parts against data everywhere but the signal region, where we would extrapolate from our fit. W+Jets: Since the signal region is defined by a top-tag, the background in mtop-mtW space behaves like multi-jet production. We could fit this background simultaneously to the QCD.

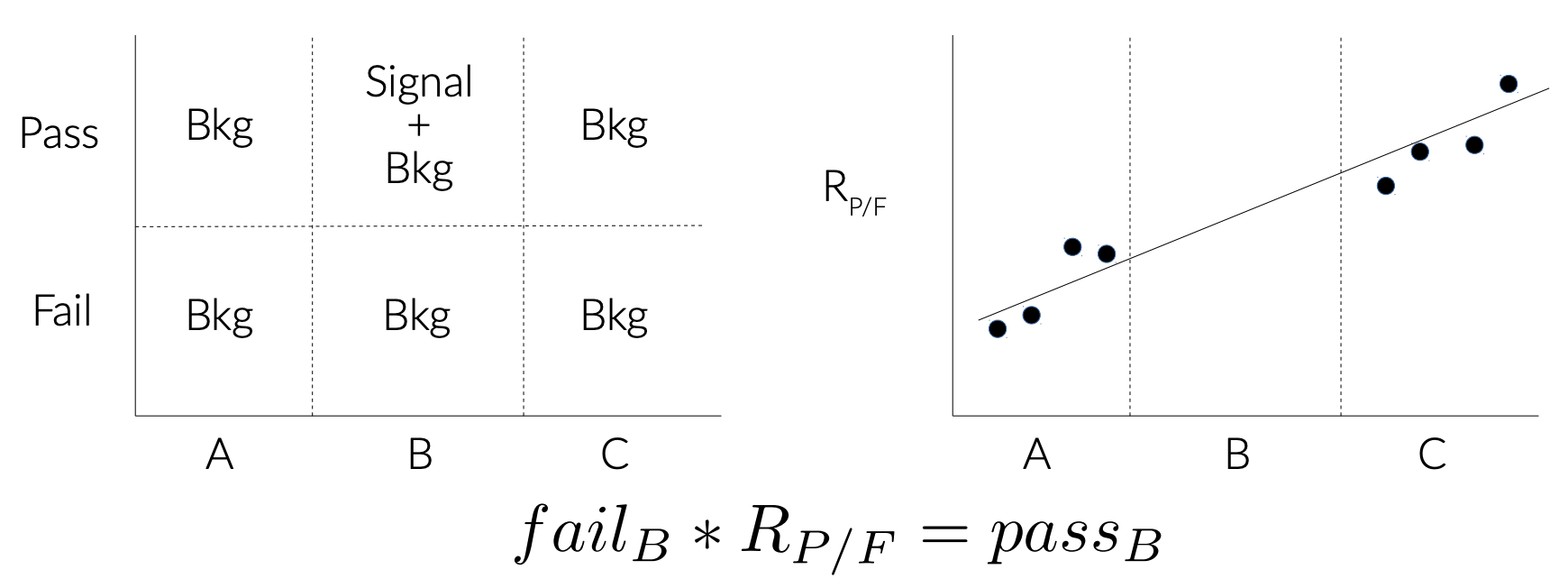
The figure below communicates how the various signal and background regions relate to each other though selections, and how (this particular) transfer function is defined from ratios of pass/fails in the regions. DataDrivenCartoon

Question: What is the variable represented here by the x-axis? What do the regions A/B/C represent, and what the are selections dividing them? What does ‘pass’ and ‘fail’ refer to?

Solution

We can start with the pass/fail, which refers to the top tag. The x-axis is mtop, meaning the regions A/B/C are different mass ranges: A is low-mass, B is the top-mass window, and C is high-mass.

Need for Data Driven Background Estimation

QCD modeling is notoriusly hard to model. One strategy to modeling processes that are not well simulated is to remove the effect of well-modeled processes from data, then creating a shape template on which to match the poor-modeled background. This approach to estimating the background is called data-driven estimation.

Question: What background processes to our signal would be good candidates for data-driven estimation?

Solution

Multi-jet QCD is almost always estimated using a data-driven technique. In addition, the W+Jets process has a QCD-formed top candidates. ttbar and singletop are relatively well-modeled, however the normalization of their distributions are allowed to float in the final parameter fit.

Validation Regions

When we obtain either a scale factor or transfer function to extrapolate from the Control Region to the Signal Region, it is often useful to have a Validation Region that lies somewhere in between these two regions where one can apply the correction to the MC and check against data to ensure good agreement. In the framework we are walking you through, the fit uses all available (non-blinded) regions to simultaneously fit the transfer function parameters, leaing no space ‘between’ the SRs and CRs to define a VR.

Blinding

One thing to keep in mind when using data before settling on final signal and control region selections is the possibility of biasing one’s methods by being exposed to the data. For example, one could imagine a situation where one is ‘testing’ methods in a signal region and then observes a ‘problem’ (lack of events, too many events, etc) which guides the analyzer to biased decision-making. A similar problem can occur if a control or validation region is chosen that has significant signal contamination. To avoid these problems, we ‘blind’ our data whenever possible. That is, we do not look at any data in the SRs, when appropriate we could also deicde to remove data if it passes a significance threshold, and ensuring the control/validation regions have little signal contamination.

Key Points

  • The backgrounds involved are processes producing jets with large pT that look like t+W.

  • All-hadronic ttbar can look like t+W if one of tops has a very soft (or untagged) b-jet. MC is reasonably modeled

  • Singletop production is sub-dominant, but irreducible. MC is reasonably modeled

  • LHC is a hadron collider, multi-jet production (QCD) is almost always a background in all hadronic analyses.

  • W/Z+Jets behaves a lot like multi-jet production since the top-tag it passes to make it into out signal selection comes from combinatoric combination of jets.

  • Control regions are used to study specific backgrounds in a kinematic region orthogonal to the signal regions; we test our background estimation in CRs and apply corrections needed there to the SR.

  • Validation regions are designed to lie orthgonal but between CRs and SRs, perhaps with lower target BG purity, to test the corrections extracted from the CR that will be applied to SRs.

  • Blinding is the convention of not looking at data in the SR (or any signal-enriched selection).

Background Estimation: 2DAlphabet

Overview

Teaching: 10 min
Exercises: 50 min
Questions

  • How are we going to estimate the background?

  • What is 2DAlphabet?

Objectives

  • Familiarize with 2DAlphabet method

Recording files of this session are in cernbox

Idea of 2D Alphabet

Normally, we do a shape hunt along some observable and measure our background is near-by kintemtic regions to estimate its expected yield in the signal region. For our case, there is a clever way to do all these tasks simultaneously. Since we are scanning across mtW, with a window designated as a Signal Region, we can use all the non-window space to fit a smooth function that extrapolates over the SR window. 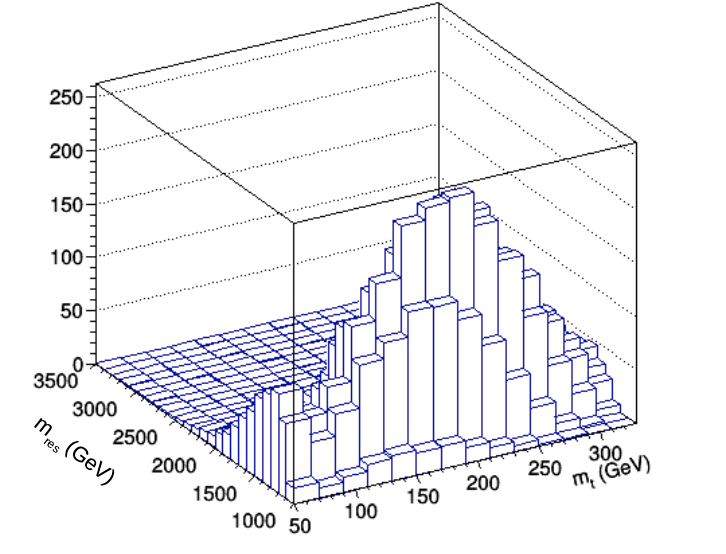2DAlphabetShape

Since we define our SR as passing exactly one top tag (most importantly with a mass window cut), we can use the adjacent region of passing 2 top tags for a ttbar/singletop constrol region. We can then use the smooth function from above to estimate the multi-jet contribution to the 2-top measurement region. Whereas the multi-jet contribution’s shape is determined by the smooth function fit, the shape of the ttbar and singletop background is set by simulation and the normalization is allowed to float.

2DAlphabetFit

Simultaneous Fit

The fitting of the multi-jet background as well as the ttbar/singletop measurement are all done simultaneously. As the multijet estimation fit optimizes, the ttbar/singletop region feeds back its normalizations to subtract from the data used in the fit optimization. We also perform the fits separately but simultaneously across years (2016-2018). In summary, the fits are done on 3 years x 2 pass/fail x 2 multi-jet/ttbar (1/2-top) = 12 2D-regions (mt, mtW).

2DAlphabetCompare

Exercise: Try Plotting CR and Get Familiar with 2DAlphabet

At tomorrow’s sessions you will dive into using 2DAlphabet for your own selections. For now, use the exisig code in BstarToTW_CMSDAS2020/examples/ex4.py to generate your own plots with selections meant for the ttbar and multi-jet CRs. You’ll need to mmodify the script and run the –select flag to make the new root files used for the plotting. As is, the script plots MC-only, can you add data to the CR plots?

Use the remaining time in the session to wrap up work in previous sessions, tomorrow we will run the 2DAlphabet framework to produce our limits. Also try looking into the 2DAlphabet framework to get an idea of how the code is structured and how you will change it tomorrow. Feel free to ask the facilitators any questions you have!

Key Points

  • We can simultaneously fit several backgrounds by defining the appropriate observables/axes, i.e. mt vs mtW.

  • 2D Alphabet is a method of fitting a polynomial function to a space (except the SR), to model the multi-jet background, and also serves as an interfae to other tools.

Tuesday DAS Plenary 10-11h

Overview

Teaching: 60 min
Exercises: 0 min
Questions
Objectives

From 10-11h there will be a DAS Plenary, please tune in to that.

Key Points

Modelling the background and signal with 2DAlphabet (a wrapper for Combine)

Overview

Teaching: 30 min
Exercises: 40 min
Questions

  • How do I use the 2DAlphabet package to model the background?

Objectives

  • Run the 2DAlphabet package

  • Apply normalisation systematics

  • Apply shape systematics

Introduction to the 2DAlphabet package

2DAlphabet uses .json configuration files. Inside of these the are areas to add uncertainties which are used inside of the combine backend. The 2DAlphabet serves as a nice interface with combine to allow the user to use the 2DAlphabet method without having to create their own custom version of combine.

A look around

The configuration files that you will be using are located in the BstarToTW_CMSDAS2020 repository in this path BstarToTW_CMSDAS2020/configs_2Dalpha/ Take a look inside one of these files, for example: input_dataBsUnblind16.json

The options section contains boolean options, some of which are 2DAlphabet specific and others which map to combine. Of the options the important ones to note are the blindedFit and blindedPlotswhich keep the signal regions blinded and in a normal analysis would keep this option true until they reached the appropriate approval stage.

The process section is basically the same as the process section in combine, but laid out in an easier to read format. Each process refers to a root file containing data or Monte Carlo simulation. A "CODE" of 1 means that the process is the data, a "CODE" of 2 means that the process is a background, and a "CODE" of 0 means that a process is a signal event. The "SYSTEMATICS" list contains the names of the systematic uncertainties for that process. The systematic uncertainties are assigned values in the "SYSTEMATIC" section. The HISTPASS and HISTFAIL refer to the pass or fail bins of a histogram. The “PASS” bin indicates the signal region whereas the “FAIL” bin indicates the multijet control region.

For more details on the sections in the configuration files, see the 2DAlphabet Documentation

Running 2DAlphabet

In order to run the 2DAlphabet package on our json configuration files, we will first make a symbolic link to the configuration files to make things easier.

# start inside the directory containing the BstarToTW_CMSDAS2020 repo
cd CMSSW_11_0_1/src/BstarToTW_CMSDAS2020/
# Now move to the directory containing the 2DAlphabet
cd ../../../CMSSW_10_6_14/src/2DAlphabet
# now create a symlink (symbolic link) to the config file directory
ln -s ../../../CMSSW_11_0_1/src/BstarToTW_CMSDAS2020/configs_2Dalpha/ configs_2Dalpha

Now run one of the configuration files.

cmsenv
# now run one of the files 
python run_MLfit.py configs_2Dalpha/input_dataBsUnblind16.json --tag=bsTest

This will create some output plots and combine cards. The output is stored in bsTest/SR16/.

Tip

If running with the configuration files for all three years, you can append --fullRun2 and that will add together the 2016, 2017, and 2018 results for the signal region and ttbar measurement region separately so that there are fewer plots to view.

Uncertainties

There are two types of systematic uncertainties that can be added to combine: normalisation uncertainties and shape uncertainties. Since this is a simplified analysis, we consider two normalisation uncertainties (luminosity and cross section) and one shape uncertainty (Top pT re-weighting) with one optional bonus exercise.

Where to add the uncertainties

Let’s take a look at adding uncertainties in the .json files. The systematic uncertainties are defined in the SYSTEMATIC section:

"SYSTEMATIC": {
    "HELP": "All systematics should be configured here. The info for them will be pulled for each process that calls each systematic. These are classified by codes 0 (symmetric, lnN), 1 (asymmetric, lnN), 2 (shape and in same file as nominal), 3 (shape and NOT in same file as nominal)",
    "lumi16": {
        "CODE": 0,
        "VAL": 1.025
    },

So in our json file, we can list a systematic and use the "CODE" to describe the type of systematic that will be used in combine. The help message describes the options. Here, lnN refers to log-normal normalisation uncertainty.

As an example take a closer look at the "lumi16" systematic. It is a symmetric uncertainty "VAL": 1.025. In this context, "VAL" refers to effect that the systematic has. In this case 1.025 means that this systematic has a 2.5% uncertainty on the yield.

For the moment, let’s just look at our symmetric uncertainties and later we will look at a shape uncertainty.

Luminosity uncertainties

As we saw in the previous example, the luminosity is a symmetric uncertainty. Each year, the amount of data collected (“luminosity”) is measured. This measurement has some uncertainty which means the uncertainty changes for each year and is uncorrelated between the years.

Discuss (5 min)

Should each Monte Carlo sample have a different luminosity uncertainty?

Solution

Monte Carlo samples for the same year should all have the same luminosity uncertainty, because the overall luminosity delivered by the detector in that year is a fixed measurement.

Cross section uncertainties

The cross section uncertainty is another symmetric uncertainty added to each Monte Carlo sample.

Discuss (5 min)

Should the signal Monte Carlo sample have a cross section uncertainty?

Solution

No. This is because the “cross section” of the signal is exactly what we want to fit for (ie. the parameter of interest/POI/r/mu)! One might ask then why we assign an uncertainty from the luminosity to the signal when the luminosity is just another normalization uncertainty. The answer is that the luminosity uncertainty is fundamentally different from the cross section uncertainties because it is correlated across all of the processes - if it goes up for one, it goes up for all. The cross section uncertainties though are per-process - the ttbar cross section can go up and the single top contribution will remain the same.

With just the luminosity and cross section uncertainties, we only have normalization uncertainties accounted for and there are certainly uncertainties which affect the shapes of distributions (our simulation is not perfect in many ways). These can be accounted for via vertical template interpolation (also called “template morphing”). The high-level explanation is that you can provide an “up” shape and a “down” shape in addition to the “nominal” and the algorithm will map “up” to +1 sigma and “down” to -1 sigma on a Gaussian constraint. The first of these “shape” uncertainties is the Top pT uncertainty.

Top pT uncertainties

The TOP group has recommendations for how to account for consistent but not-understood disagreements in the top pT spectrum between ttbar simulation and ttbar in data (see this twiki for more information). This analysis falls into Case 3.1 from that twiki. The short version of the recommendation is that one should measure the top pT spectrum in a dedicated ttbar control region which is exactly what the ttbar measurement region of the analysis is for.

For this analysis the top jet mass window is 105-220 GeV which constrains the ttbar background but does not leave a lot of room to work with when blinded. Fortunately, mtt is correlated with top pT so we can just measure the correction in the 2D space while also fitting for QCD and all of the other systematics in the ttbar measurement region and signal region!

Bonus: Analysis details on decisions

The decision of the correction for the ttbar top pT spectrum was pretty simple. We just took the functional form (for POWHEG+Pythia8) farther down and rewrote it as e(α0.0615 - β0.0005*pT) where α and β are nominally 1 (so just the regular correction on that page). Then each α and β are individually varied to 0.5 and 1.5 to be our uncertainty templates for the vertical interpolation. These are what are assigned to Tpt-alpha and Tpt-beta. For example, if the post-fit value of Tpt-alpha was 1 and Tpt-beta was -1, the final effective form of our Tpt reweighting function would be e(1.50.0615 - 0.50.0005*pT).

Exercise (20 min)

Add the Top pT uncertainties to the appropriate processes and see the changes in combine.

The uncertainties are already included in the section on "SYSTEMATICS". However, they have not been added to the individual processes. To start this exercise, add the Tpt-alpha and Tpt-beta uncertainties to the appropriate processes. Which processes should these uncertainties be added to? Then add in the the uncertainties to the appropriate processes and rerun the 2DAlphabet. Compare the combine cards using diff to see the changes before and after adding in the top pT uncertainty.

Do this exercise for input_dataBsUnblind16.json and then after looking at the solution, apply to the other config files.

Solution

The Top pT uncertainties should be applied to the ttbar and ttbar-semilep processes. For example:

"ttbar": {
    "TITLE":"t#bar{t}",
    "FILE":"path/TWpreselection16_ttbar_tau32medium_ttbar.root",
    "HISTPASS":"MtwvMtPass",
    "HISTFAIL":"MtwvMtFail",
    "SYSTEMATICS":["lumi16","ttbar_xsec","Tpt-alpha","Tpt-beta"],
    "COLOR": 2,
    "CODE": 2
}

Now, keep the data card made before doing this change and then run the code to see the difference.

# From the 2DAlphabet directory, store the old card
cp bsTest/SR16/card_SR16.txt no_topUn_SR16.txt
# Then, rerun the 2DAlphabet
python run_MLfit.py configs_2Dalpha/input_dataBsUnblind16.json --tag=bsTest
# Then look at the difference
diff no_topUn_SR16.txt bsTest/SR16/card_SR16.txt

To understand more about what is happening in combine and how this shape uncertainty is applied see this DAS exercise

Now that this change has been made for one process in one configuration file, apply the same change for all ttbar and ttbar-semilep processes in all 6 configuration files.

Note that ttbar is all-inclusive for 2016 and hadronic only for 2017 and 2018 so the ttbar_semilep is included only in 2017 and 2018.

Bonus Exercise: Trigger Efficiency uncertainty

The trigger efficiency uncertainty is defined as a systematic in the configuration files. As a bonus exercise, add this shape systematic uncertainty to the processes. How do you measure Trigger efficiency? And how is this uncertainty calculated?

This exercise is a bonus and not necessary to continue on.

Key Points

  • Luminosity uncertainties affect all processes equally

  • Cross section uncertainties should not be applied to signal

  • Template morphing is used to determine shape uncertainties

Tuesday Lunch 12-13h

Overview

Teaching: 0 min
Exercises: 60 min
Questions
Objectives

Enjoy your lunch from 12-13h :)

Key Points

Obtaining upper cross section limits

Overview

Teaching: 10 min
Exercises: 50 min
Questions

  • How do we use the 2DAlphabet package to set limits?

  • Once I unblind, did we find new physics? If not, what can we say?

Objectives

  • Use the 2DAlphabet package to set limits

  • Provide expected sensitivity (upper cross-section limits) before unblinding as a function of resonance mass.

  • Unblind and compare observed to expected limits.

Limits!

This is one of the big milestones in an analysis, setting limits! After un-blinding the limit plot, you can see if you discovered new physics.

Running the limit setting program

The limit setting program for 2DAlphabet needs to be run for each mass point under consideration and for each year. The fitting program must be run on each year before the limit program can be run. So make sure that you completed the exercise from the Modeling exercise that uses run_MLfit.py.

Make Limits

First run the limit program for each of the mass points. There are 19 mass points between 1400 and 4000 (1400, 1600, …), so it might be a good idea for each of you to choose 4 mass points to do and then combine the results together.

python run_Limit.py configs_2Dalpha/input_data*.json --tag=LimitLH1400 --unblindData -d <name of dir from ML fit> signalLH2400:signalLH1400 --freezeFail
  • The directory we used in the previous example was bsTest so replace <name of dir from ML fit> with bsTest (or whatever you choose to name it).
  • tag is the name of the output directory.
  • “signalLH2400:signalLH1400” allows us to find:replace any strigns in the configs (this is useful for swapping out one signal sample for another without having to write a new set of configs - in this case, “signalLH2400” is replaced with “signalLH1400”).
  • --freezeFail which will set the “fail” bins to their post-fit values and then make them constant.
  • optionally unblind with --unblindData.
python set_limit.py -s signals.txt --unblind

The signals.txt file uses commas and new lines to seperate the information. Here is an example for just three mass points.

LimitLH1400,  LimitLH1600,  LimitLH1800
1400,         1600,         1800
0.7848,       0.3431,       0.1588
1.0,          0.1,          0.1

Here are the meaning of the rows in order:

  • Folder location where higgsCombineTest.AsymptoticLimits.mH120.root lives (this would be your –tag from the run_MLfit.py step)
  • Mass in GeV
  • Theoretical cross section for the theory line
  • Normalized cross section (values stored in bstar_config.json)

Now use these steps to run the limit setting program on all 19 mass points.

Understanding the limits

Did you discover new physics? How do you know?

Key Points

  • We can define expected sensitivity of an analysis with simulation-only by assuming the data expected will be exactly what the background estimation predicts.

  • We combine the systematic variations as a 1/2-sigma envelope around nominal expectation to quantify the confidence of our measurement.

  • After unblinding, if we have a down-fluctuation of data the expected exclusion appears stronger and vice-versa with up-fluctuations and apparently weak exclusions.

Bonus: Calibrating a jet subtructure tagger.

Overview

Teaching: 15 min
Exercises: 45 min
Questions

  • How can I validate a jet substructure tagger in data?

  • What can be done if a tagger (object-selection technique) performs differently in data vs simulation?

Objectives

  • Implement a selection that is enriched in boosted W bosons and top quarks.

  • Extract efficiency scale factors.

Key Points

  • We can define tagger scale factors by measuring the efficiency of the tagger in t+W enriched regions.

DAS Presentations

Overview

Teaching: 0 min
Exercises: 300 min
Questions
Objectives

Get your presentations together and show the rest of DAS what you’ve been working on!

Key Points